Introduction
Man has used hierarchical decomposition for thousands of years to classify objects and artifacts, to structure organizations, to plan activities, to describe physical and conceptual configurations, or to organize knowledge and events. Such structures are inevitably manifested in dimensional information models as taxonomies of products, customer segmentations, organizational and location hierarchies, cost and account decompositions, component breakdowns, genealogy trees, program structures, to mention only a few. For the purposes of this article, we will consider all such hierarchical (tree) dimensions that have the following characteristics:
1. They are defined over some object class
(nodes) participating in a binary relationship type (arcs) forming a tree
graph; i.e. each node has at most one parent and potentially many children.
Different branches of the tree may have different depth. Multiple roots can be
viewed as children of a null parent, making a single tree with a null root.
2. The binary relationship that defines the
graph is a step relationship such as
“is parent of”, “immediately
reports to” or “is part of”.
Dimensions often have a classifying criterion (reporting, containment etc.),
however explicit hierarchies are suited for arbitrary segmentation hierarchies
such as those used to classify markets or customers, where the classification
rules vary from branch to branch and level to level.
3. A transitive relationship can be
recursively defined by chaining these step relationships in sequence. The set of all such transitive relationships
that can be generated is the transitive closure. For example, we can define the ancestor as either being a parent,
or an ancestor of a parent. This is the same as defining
ancestors as parents, parents of parents, parents of parents of parents, and so
on. Similarly, we can define reports to as the relationship between
any two organizations that are connected by a chain of directly reports to relationships. Finally, the includes/is used in relationship is
similarly derived as a chain of part of
relationships.
From now on, instead of abstract constructs, we will use the organization and the reporting relationship to illustrate the design of recursive dimensions that can be efficiently queried for transitive closure. These queries can be used in isolation or as a dimension filter combined into a larger query. The Conclusion contains some additional thoughts on when to use recursive hierarchies and what to watch for.
Our design will represent the organization as a hierarchical dimension with one (or more) top nodes, which decompose down to elementary ones, recursively via the relationship reports to. The following relation identifies such an organizational entity:
org(TID,
PID, NAME, other properties...)
TID is the “token ID” serving as the surrogate name of the organization dimension. The PID is the “Parent ID”, denoting a reference to the parent organization. Since this is a hierarchical structure, at most one parent per node is possible. The highest level organizations will have no parent; i.e. the PID can be either NULL or the default value. For the purposes of our example, we will assume the use of numeric TIDs and PIDs and the use of NULL in the top node PIDs to denote “no parent”.
A typical problem is to select all organizations directly or indirectly reporting to a given organization, or to select all organizations to which a given one (or small list) directly or indirectly reports to. This operation is particularly useful as a dimension filter if it can be combined with other dimension filters and joined to a fact in one SQL statement. The example in figure 1 shows the direct reporting relationships. Assume that we need to extract all expenses incurred by organizations under organization X. Two obvious approaches to solving the problem are to traverse the structure, or to pre-store the transitive closure relationship in a table. The traversing of the structure can be achieved either by SQL extensions, such as the “Connect By” clause in Oracle, or a recursive union of the DB2 family. This can also be done procedurally, by reading successive layers of children of the organizations within X, but procedures can not be used as part of larger SQL queries.
The “prestored transitive closure” approach involves an intermediate table that stores all descendents of X, and a join to the org table. The intermediate table can be temporary, generated every time a query is issued, or permanent, always containing the transitive closure of the "reports to" relationship.
Each of these solutions has its own disadvantages: The first one actually “walks the structure” requiring multiple requests to extract children sets for each node retrieved. The advantage of this approach is that it does not introduce any update anomalies since no redundant data is maintained. The second solution uses set processing, but it requires that a temporary table be first built (and indexed) or one must permanently maintain a very large redundant table and deal with the associated update anomalies. A tree five layers deep with a fanout of 10 children per node has a total of 11,111 nodes, 11,110 parent-child relationships, but its transitive closure contains over 11,000,000 ancestor descendent relationships. A single maintenance operation may affect over one million of these ancestor descendent relationships. The cost of this approach grows geometrically as the fanout and depth grows. The maintenance complications and lack of scalability make this option undesirable.
Before discussing a better alternative, it is worth considering yet another interesting problem: “Given two organizations, verify that directly or indirectly one reports to the other”. The structure traversal would require comparing all the descendents and ancestors of the first organization to the second. A better approach would be to take the ancestor path to the top from each of the two nodes and verify if the other node is in it. The cost will then be less than 2h where h is the maximum depth of the organizational tree. Alternatively, it would require searching for the existence of the pair in the transitive closure set, if physically maintained. A generalization of this variant of dimension filtering selects nodes using both ancestor and descendent set qualification: “select all departments that belong to these divisions and have offices at these locations” or “select all market segment/locations of college students with at least 50% state college participation”.
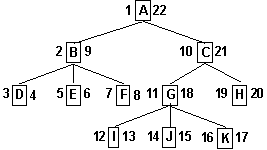
Figure 1----A Tree Graph with S & S2 Numbers
The problem with these graph-selections is the impracticality of maintaining large redundant transitive closure tables, or the low performance of path traversal using recursive SQL extensions. Fortunately, there is an alternative, that uses an old idea, topological ordering, to pre-enumerate the nodes at maintenance time, so that ancestor-descendent queries can be simple and fast.
The LR Design Approach
Observe the tree in figure 1. Let the nodes represent org entities, and let arcs denote "immediately reports to” relations. Notice the two numbers that lie on the left and right of each node. Can you see how they can be used to identify all ancestor-descendant relations? Check how each node's numbers are between the left and right number of each of their ancestors. In addition, a node's two numbers define the outside boundaries of all their descendants' numbers.
Let's call these two numbers L and R for the left and right one respectively. These attributes encode the hierarchical ordering of the organizational entity in the whole hierarchy in a way that can be used in set queries. Here are the rules that govern their use:
1. L
and R share a common domain of
ordered values. This domain is chosen
to be a binary integer. A given value of this domain can be used only once,
either as an L or an R value but not as both an L and an R value. For a given node, the L
value shall be strictly less than the R
value
2. L
and R, although unique, they shall
not be used for external identification of any entity, like we never use Row
IDs to reference a row in a table. They can be arbitrarily reassigned to better
facilitate efficient retrieval, in the same spirit that tables and indexes may
be reorganized to facilitate efficient retrieval.
3. Any two nodes satisfy the
ancestor-descendent relationship exactly when the descendent's L (or R) value is between the ancestor's L and R values:
![]()
![]()
Simply, all L and R values of nodes hierarchically
subordinate to a given node, are between its L and R range, and no
node that is not hierarchically subordinate to it satisfies this property. For example if l and r are the
respective L and R values of some organization, then all
organizations directly or indirectly reporting to it will have their L between l and r.
The L and R numbers can be viewed as intervals. Each parent’s interval covers the sum of the intervals of all its children. These intervals define a topological ordering over the nodes. The assignment of L/R values is the result of numbering the nodes of a tree depth-first, traversing the nodes from left to right. During the enumeration process, each node is visited coming once from the top and a second and last time from below, after visiting all its descendents. At these two visits, the L and R attributes are set respectively, assigned next sequential values dispensed off a counter. Figure 1 shows this numbering sequence.
Figure 2 shows two queries and a view. Case 1 returns the ancestors, and case 2 returns the descendents of the node named QNAME. Two references are made to the same table, ‘A’ being the correlation name for the “ancestor” role, and ‘D’ being the “descendent” role. All queries use the same predicate to restrict the descendent nodes’ L values to fall in the (A.L..A.R) range.
Figure2----Tree Queries
case 1:
Query of organization ancestors of QNAME (reporting chain up)
select
A.NAME, . . .
from
ORG A, ORG D
where D.NAME
= :QNAME and
D.L
between A.L and
A.R
Case2: Query returning set of all direct
and indirect reports to node identified by :QNAME as of :QDATE:
select
D.NAME, . . .
from
ORG A, ORG D
where A.NAME
= :QNAME and
D.L between
A.L and A.R
Case 3:
View returning ANAMEs of ancestors of :descendents DNAME as of :QDATE;
create
view org_anc
(DNAME, ANAME, . . .) as
select
D.NAME,
A.NAME . . .
from
ORG A, ORG D
where D.L between A.L
and A.R
Case 3 shows a view that relates descendents and ancestors. This view can be used either to return sets of ancestors by descendent given a set of descendents, or sets of descendents by ancestor given a set of ancestors. If we were to physically store this table, it would have the contents of the transitive closure table discussed in the Introduction. Instead of joining the transitive closure table, we will use the “between” predicate to do the filtering for us. Having faith in the optimizer, the DBMS will push selections through the view to develop a plan equivalent to case 1 or 2.
An often-posed question is “Why don’t we use a hierarchical keyword to achieve the same result?” For example, an IP address like scheme could enumerate the levels like 1,1.1,1.2,1.3,1.1.1 etc. The problem with this scheme is that all qualifications need to start from the top. Otherwise, we will have to scan the whole index or table. With the L/R enumeration however, we can relate any node to any other and still employ index scans.
Performance of the L/R Method
Descendent seeking queries are the most efficient. Ancestor seeking ones can be reduced to half an index-only scan. A combined index on L (descending), R (ascending) helps ancestor searches. The between predicate for this type of search has an unusual form, restricting a constant between two columns. This situation will result in a matching lookup of the descendent’s L value on the combined index, and a scan to the end of the index. The best we can achieve in this case is to use index only access. The average cost of this query will be that of scanning half the index since every value in the domain of L is equally likely for the constant.
For the more common descendent-seeking queries, the selected rows qualify whenever their L is between two constants, i.e. the L and R of the given ancestor. Such a query will consequently use a matching lookup, to locate the lower bound of the "between", and scan the index until the upper bound is reached. These queries are very efficient, since all scanned index entries qualify.
The performance advantage of the L/R method over the SQL recursive union or Connect By clause is about a level of magnitude. This advantage is because most of the work is done up-front, and the topological ordering of the nodes is already accomplished and captured in the L/R interval indexing. Here are a few points on the L/R performance:
1. To detect whether two nodes have an ancestor-descendent relationship normally requires the traversal of the path from one node to the other. Using the L/R numbers however, any two nodes can be tested by using a simple between clause without traversing the graph.
3. L/R descendant selection subqueries scale well, even in MPP share-nothing environments. The simple ancestor-descendent range test is partitionable and can be combined with other partitionable filtering predicates; thus achieving distributed dimension qualification. Recursive SQL requires multiple directed invocations of the children-seeking query before applying other predicates. This approach pays for latency delay roughly proportional to the depth of the traversed tree, in addition to the implication discussed under item 2 above.
Using L/R Dimensions in Star
Joins
Let’s see how the subqueries we discussed over isolated dimensions can be integrated into fact joins with multiple dimensions. We will have to extend the example with a fact table, say one that captures financial data: cost(ORG, TYPE, PERIOD, AMT). It references lowest level nodes of the organizational hierarchy, a type hierarchy and a time period hierarchy, and captures the period amount as a metric. For every period, organization and type, a fact is recorded. The schema for our little example is described at the top of figure 3. Next are the definitions of ORG_TC and TYPE_TC views that capture the transitive closure as described earlier for the organization (ORG) and cost type (TYPE) dimensions respectively. These views contain the attributes for each ancestor and each descendent pair, prefixed with A and D respectively.
Figure 3
----Dimensions in Context
Schema:
org
TID,
PID, NAME, L, R, LEVEL . . .
type TID,
PID, NAME, L, R, CLASS, POSTING?
period WK_END_DT,
MONTH, YEAR
cost ORG,
TYPE, PERIOD, AMT
Transitive
Closure Views:
create
view org_tc
(DTID,DNAME, ATID,ANAME, . .
.) as
select
D.TID,D.NAME,
A.TID, A.NAME . . .
from
ORG A, ORG D
where D.L between A.L
and A.R
create
view type_tc
(DTID,DNAME, ATID,ANAME, ...)
as
select
D.TID,D.NAME,
A.TID, A.NAME . . .
from
TYPE A, TYPE D
where D.L between A.L
and A.R
Query
using Views:
select
O.ANAME,
T.ANAME,P.MONTH,sum(AMT)
from
ORG_TC O, TYPE_TC T,
PERIOD P, COST C
where P.WK_END_DT
between 1/1/1998 and 8/1/1998
and O.ALEVEL
= ‘DEPT’
and T.DCLASS = ‘LABOR’
and T.ALEVEL
= ‘S’
and P.WK_END_DT
= C.PERIOD
and T.TID = C.TYPE
and O.TID = C.ORG
group
by O.ANAME, T.ANAME, P.MONTH
order
by 3,1,2
Query
using nested SQL:
With
ORG_TC as (select distinct D.TID, A.NAME
from ORG A, ORG
D
where D.L between A.L
and A.R
and A.LEVEL =
‘DEPT’ ),
TYPE_TC as (select distinct D.TID,A.NAME
from TYPE A, TYPE
D
where D.L between A.L
and A.R
and D.CLASS = ‘LABOR’
and
A.LEVEL = ‘S’)
select
O.NAME,
T.NAME,P.MONTH,sum(AMT)
from
ORG_TC O, TYPE_TC T,
PERIOD P, COST C
where P.WK_END_DT
between 1/1/1998 and 8/1/1998
and P.WK_END_DT = C.PERIOD
and T.TID = C.TYPE
and O.TID = C.ORG
group
by O. NAME, T. NAME, P.MONTH
order
by 3,1,2
Let’s assume that we are seeking all labor charges grouped by month, at the summary cost type level (TYPE.LEVEL = ‘S’) and department level of the organization. Two forms of the query are shown. The first one uses the transitive closure views, while the second exploits nested SQL and the “WITH” clause of the SQL3 proposal. The first implementation would be appropriate for any DBMS with an optimizer that will avoid unnecessary view materialization, such as Oracle. The second form is currently supported by the DB2 family, and with slight modification, it can be implemented using temporary intermediate tables in Sybase.
Of course, a straightforward implementation without views or nested SQL is also possible, however it will expose two uses of ORG and of TYPE tables to the user or tool that has to write the query. The nested SQL suffers from the same problem, but because of the modularity allowed by the in-line views (WITH clause); it is easier to compose by advanced users, or by tools using template-driven engines.
A complication that may arise is that dimension selections contain no duplicates during the join to the fact table. One can often guarantee this from the selection criteria alone. In cases, however, where lists of ancestors are provided, it may be that some are descendents of others, and we may end up selecting the same descendent multiple times. The nested SQL example of figure 3 uses the DISTINCT keyword in dimension subselects to gurantee the elimination of duplicates. Regular queries can also achieve the same result by pushing the selection in EXISTS or IN clauses.
Generating L and R numbers
We saw how the L/R numbers can be used for efficient ancestor-descendant queries. However, how should these values be maintained? It can be done incrementally, as the table is updated, or in batch. Figure 4 describes a simple algorithm that assigns these numbers. It uses the parent-child relationship to walk the hierarchy from the root(s) depth-first, left-to-right, and assigns values to L and R using a simple counter. In order to allow for efficient maintenance operations, a constant SKIP-VALUE is added prior to assigning the R value. This has an effect similar to that of PERCENT_FREE in an index. On-line maintenance activities use the range of unused L values to attach or reallocate children. After a while these ranges are filled, and a batch reassignment has an effect similar to that of index reorganization. By allowing neither L nor R to be used for externally referencing objects, this reassignment remains independent to object identification and referencing. To carry the indexing similarity a step further, think how by not using addresses to reference objects in an R-DBMS index, maintenance remains orthogonal to object identification.
The algorithm starts by reading all nodes that have no parent, and storing them in an array. The last array element is assigned the L value from an incremented counter, and then all its children are appended to the array. The last element is again selected and processed similarly, and this is repeated until some element is found that has no children. The array now contains concatenated consecutive children sets along one path of nodes defined by the lexicographically highest keys of each level.
Figure 4----
L & R Generation Algorithm
accept constant SKIP;
let A:
array of { TID: primary key of org,
L:
integer = 0,
R: integer = 0}
indexed by i = 0;
initialize
integer: Counter = 0 ;
load root nodes using
select TID,
0, 0
from
ORG
where PID
is NULL ;
load
each into A after incrementing i by 1
-- i is left pointing to the last element loaded
while i > 0 do -- process last node of
array until empty:
if A[i].L
= 0
set A[i].L := ++ Counter;
append children of A[i].TID to
A using
select TID, 0. 0
from ORG
where PID = A[i].TID
load each into A after incrementing i by 1
--
i is left pointing to last element
loaded
else
set A[i].R := (Counter :=
Counter + SKIP);
update
ORG[TIDi] using
update ORG
set L = A[i].L
R = A[i].R
where TID = A[i].TID
decrement i by 1
endif
repeat;
Then the R number of the last childless element is assigned, after incrementing the counter by the constant SKIP value, and finally its L and R-values are updated in the database. Processing then continues with the next item on the left in the array. If that item has not been assigned an L value, it is a member of the same child-set, and follows the same processing, that is, its children are appended to the right and processing continues with the last element. If on the other hand the item already has an L value assigned, it means that all its children have been processed and stored. The next counter value is assigned to its R, and the node is written to the database before proceeding with the next node on the left.
Each time the while loop is entered, the following applies:
1. All ancestors of any node on the array are somewhere between the beginning of the array and that node.
2. If a node on the array has been assigned an
L number, all its ancestors have been assigned smaller L values.
3. If A[i] has an L number assigned, it has no
children, or its children have been updated with L values higher than
A[i].L and lower than or equal to the
Counter value. Also, all its ancestors have been assigned smaller L values,
and none of them has been assigned an R
value
The process eventually unwinds until no nodes are left on the array unprocessed. The array size needed is equal to the maximum combined size of all children sets along any one path from any top to any leaf node.
The algorithm uses the array as a stack to process the tree in layers. Each node is read once and updated once, consequently the cost of the algorithm is of the order of the number of nodes in the tree.
A way to improve the performance of this algorithm is to reduce the cost of attempting to access the children of leaf nodes. This can be achieved by marking all nodes that are leaves up-front, using two set update operations that assign the appropriate value to the LL (Lowest Level) indicator:
Update ORG set
LL = Y;
Update ORG set LL = N where ORG.TID not used as a PID
The cost of this enhancement is two table scans and can only be justified if the number of leaf nodes is significantly larger than the non-leaf ones. In a tree such as the example discussed in the introduction, this would amount to executing the second set update for only 1,111 nodes, and in exchange avoid 10,000 attempts to get children of leaf nodes.
A word of caution: This algorithm assumes that the PID references do not form cyclic paths. If the purity of the tree can be guaranteed from the process that inserts/updates the table and the PID value, the algorithm shown will be adequate. Otherwise an “occurs check” needs to be added to insure that every time a new layer of children is read into the array A, none of these children also appears in their respective ancestor path.
Conclusion
The technique described in this article is not a general substitute for fixed level dimensions or hierarchies. Fixed depth dimensions are simpler to implement, maintain and query. However, there are cases where forcing a dimension to a fixed uniform number of levels causes more problems than it solves. Hierarchies that have variable depth or an uncertain number of levels or hierarchies defined after the warehouse is deployed, or stratifications that are based on complex rules can often benefit if implemented as recursive hierarchies.
Remember that recursive hierarchies are desirable for their flexibility, they are less of a performance concern, but they introduce some degree of complexity. Make sure that your front-end tools will generate the proper SQL and that you have worked out a way to maintain them. Validate performance expectations with your specific DBMS and optimizer using realistic size dimension and fact tables.
Recursive hierarchies can also implement slowly changing recursive dimensions using versioning. The result is a very powerful, general dimension archetype. The hierarchical behavior and the versioning behavior can be captured as independent design patterns and can be superimposed. The versioning approach was presented in the DBP&D article on “Snapshot Integrity” in the September 1998 issue.